第一行包含一个整数n,表示开始时平面上圆的数量,
接下来n行,每行包含三个整数xi,yi,ri,描述圆ci圆心的xy坐标和它的半径。
-1e9<=xi,yi<=1e9, 1<=ri<=1e9
1<=n<=3e5
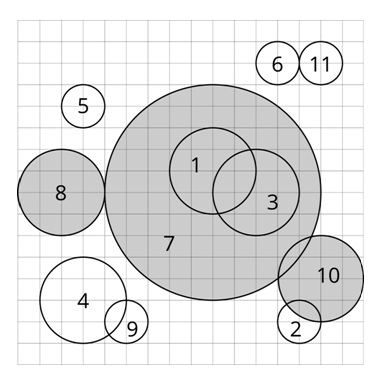
11
9 9 2
13 2 1
11 8 2
3 3 2
3 12 1
12 14 1
9 8 5
2 8 2
5 2 1
14 4 2
14 14 1
7 2 7 4 5 6 7 7 4 7 6
//题目描述中的图片对应了样例中的情形。