第1行包含两个整数N和M (1<=N<=100,000,2<=M<=30),
第2行包含一个有N个数字的串S0。
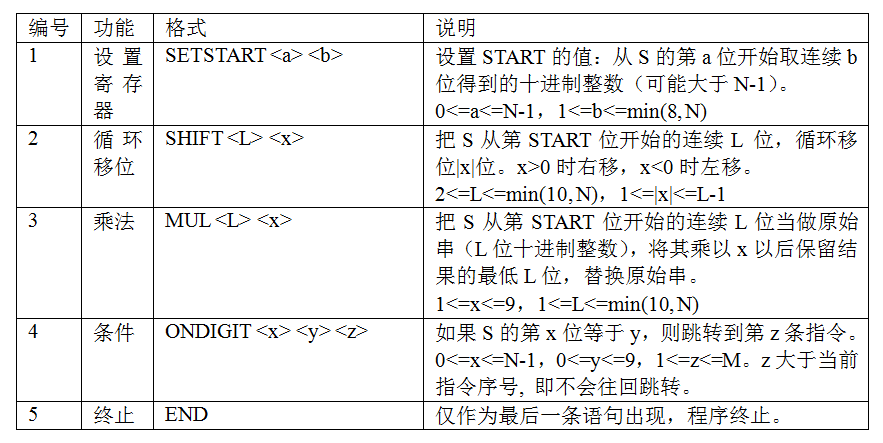
第3行到第M+2行为一段程序,每行一条指令,程序保证无错,行末和行首均没有空格。
.png)
4 5
1234
MUL 3 2
SETSTART 2 1
ONDIGIT 0 4 1
SHIFT 3 –2
END
8
//该样例对应于题目描述中给出的示例程序。前29次生产出来的项链是:
4426 4886 6796 8356 0676 4136 6286 6526 4306 0866
6712 2432 4882 2796 8556 0716 6412 2822 4562 2192
2786 6556 0316 6602 0322 4062 2182 4382 2786…
可以看出,从2786开始机器陷入了循环,因此从2786开始的8条项链将被无限制的生产出来。