在Pty学校附近,有一座名之为岳之麓的高山。Pty很喜欢和(哔——)一起爬山。
山的平面模型如下:
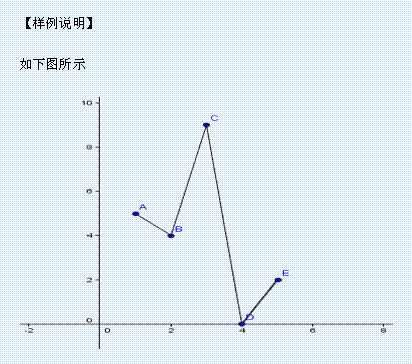
山由一个顶点集:A1,A2…An给定,保证Ai的x单调递增。我们将Ai和Ai+1之间连上线段,表示山的某一段。如下图所示:
Pty想要爬到这座山的最高的顶点,当两个顶点的高度相同时,我们认为x比较大的顶点要高一些。Pty不是盲人,所以他将会在爬山时采取一些策略,使得他能够尽量快的到达最高的顶点。
Pty从初始的顶点出发,往左右看去,他将朝他能够看到的最高的顶点方向走去。当走到每一个顶点时,他都会重新观察,如果这时看到的顶点比之前看到的顶点还要高,那么他将选择此时看到的顶点走去,直到他到达最高点为止。
例如上图中:Pty从A4点出发。他能够看到的最高点是A6,所以他将会向右侧走去。当他到达A5号点时,能够看到A1点比A6点更高,所以他会调转方向,向左侧走去。由于A1是最高的顶点,所以他将一直往左侧走,直到到达A1为止。
Pty想知道从每一个顶点出发,分别需要走过多少段才能到达最高点。例如上图中从A4出发需要走过5段才能到达最高点。